CIRI-CIRI BILANGAN HABIS DIBAGI

Dengan mengetahui ciri-ciri suatu bilangan habis dibagi dengan suatu bilangan tertentu, maka akan memudahkan kita dalam melakukan perhitungan-perhitungan tertentu, misalkan saat menyederhanakan pembilang dan penyebut suatu pecahan.

Ciri-ciri bilangan habis dibagi 2
Suatu bilangan habis di bagi dua apabila memiliki angka satuan 0, 2, 4, 6, 8. dengan kata lain, bilangan tersebut adalah bilangan genap.
contoh :
12348, adalah bilangan yang habis dibagi 2 karena memiliki satuan 8 yang berarti merupakan bilangan genap
24687, adalah bilangan yang tidak habis dibagi 2 karena memiliki satuan 7 yang berarti merupkan bilangan ganjil

Ciri-ciri bilangan habis dibagi 3
Suatu bilangan habis dibagi 3 apabila jumlah angka-angka penyusun bilangan tersebut merupakan kelipatan dari 3.
contoh :
1237212 adalah bilangan yang habis dibagi 3, karena 1+2+3+7+2+1+2 = 18 dan 18 merupakan kelipatan 3
36937 adalah bilangan yang tidak habis 3, karena 3+6+9+3+7 = 28 dan 28 bukanlah bilangan kelipatan 3

Ciri-ciri bilangan habis dibagi 4
Suatu bilangan habis dibagi 4 apabila 2 digit terakhir dari bilangan tersebut bisa dibagi 4
contoh :
1000004 adalah bilangan yang habis dibagi 4, karena dua digit terkhir yakni 04 adalah bilangan yang habis dibagi 4
484442 adalah bilangan yang tidak habis dibagi 4, karena 2 digit terakhir yakni 42 adalah bilangan yang tidak habis dibagi 4.

Ciri-ciri Bilangan habis dibagi 5
Suatu bilangan habis dibagi 5 apabila digit terakhir atau angka satuannya adalah angka 0 atau 5.
contoh :
12345 adalah bilangan yang habis dibagi 5 karena memiliki satuan 5
1112300 adalah bilangan yang habis dibagi 0 karena memiliki satuan 0
505053 bukan bilangan yang habis dibagi 5 karena memiliki angka satuan 3 (bukan 0 dan bukan 5)

Ciri-ciri Bilangan habis dibagi 6
Suatu bilangan habis dibagi 6 apabila bilangan tersebut genap dan habis dibagi 3
contoh :
12246 adalah bilangan yang habis dibagi 6, karena bilangan tersebut genap dan 1+2+2+4+6 =15 yang berarti habis dibagi 3
12243 adalah bilangan yang tidak habis dibagi 6, karena meskipun 1+2+2+4+3 =12 yang berarti habis dibagi 3, akan tetapi bilangan tersebut ganjil
4246 juga adalah bilangan yang tidak habis dibagi 6, karena meskipun genap akan tetapi 4+2+4+6 = 16 yang berarti tidak habis dibagi 3

Ciri-ciri Bilangan habis dibagi 7
Suatu bilangan habis dibagi 7 apabila digit terakhir dikali 2 dijadikan pengurang bilangan di depannya menhasilkan kelipatan 7.
contoh :
308 adalah bilangan yang habis dibagi 7, karena 30 -(8x2) = 30 -16 =14 merupakan kelipatan 7
406 adalah bilangan yang habis dibagi 7, karena 40 - (6x2) = 40 =12 =28 merupakan kelipatan 7


Ciri-ciri bilangan habis dibagi 8
Suatu bilangan habis dibagi 8 apabila 3 digit terakhir bilangan tersebut habis dibagi 8
contoh :
2008 adalah bilangan yang habis dibagi 8, karena 008 adalah bilangan yang habis dibagi 8
2016 adalah juga merupakan bilangan yang habis dibagi 8, karena 016 habis dibagi 8

Ciri-ciri bilangan habis dibagi 9
Suatu bilangan habis dibagi 9 apabila jumlah angka-angka penyusunnya habis dibagi 9
Contoh :
1233, adalah bilangan yang habis dibagi 9, karena 1+2+3+3=9 dan 9 habis dibagi 9
4231125 juga adalah bilangan yang habis dibagi 9, karena 4+2+3+1+1+2+5 = 18 dan 18 habis dibagi 9

Selamat menggunakannya untuk mempermudah anda dalam menyederhanakan pecahan.



Note : Tulisan ini terinspirasi dari tulisan Ali Khan Su'ud

Mengapa Bilangan Negatif dikalikan dengan Bilangan Negatif Menghasilkan Bilangan Positif????

??????? APA IYA TAH?????

Pengalaman saya mengajar matematika SMK selama beberapa tahun, selalu saja ada siswa yang kritis dalam bertanya. Salah satu pertanyaan yang pernah beberapa kali dilontarkan oleh siswa saya adalah, 'MENGAPA BILANGAN NEGATIF DIKALIKAN BILANGAN NEGATIF MENGHASILKAN BILANGAN POSITIF??' Agar tetap bisa mempertahankan minat terhadap Matematika, maka saya akan mencoba menuliskan pembuktian dari pertanyaan tersebut. Saya berharap semoga tulisan ini bermanfaat terutama bagi siswa-siswa saya.

Hal yang akan kita tunjukkan adalah
- bilangan positif dikalikan positif hasilnya adalah positif
- bilangan positif dikalikan negatif dan sebaliknya hasilnya adalah negatif
- terakhir, bilangan negatif dikalikan bilangan negatif, hasilnya justru adalah positif.

Dengan menggunakan definisi dari perkalian 2 bilangan, yaitu
a x b =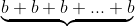 , a dan b adalah sebarang bilangan
sebanyak a kali
Contoh : misalkan 3 x 5 = 5 + 5 + 5 = 15, maka jelaslah bilangan positif dikalikan bilangan positif hasilnya adalah positif

Masih menggunakan definisi perkalian 2 bilangan,

a x (-b) =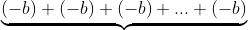 , a dan b adalah sebarang bilangan
Sebanyak a kali

Contoh : misalkan 3 x -5 = (-5) + (-5) + (-5) = -15, maka jelaslah bilangan positif dikalikan bilangan negatif hasilnya adalah negatif.
Bagaimana jikalau soal dibalik, misalkan -3 x 5 ? ingat bahwa berlaku sifat komutatif pada perkalian. Jadi -3 x 5 = 5 x -3 = (-3) + (-3) + (-3) + (-3) + (-3) = -15

Penjelasan berikutnya, sampailah pada inti permasalahan yaitu bahwa bilangan negatif dikalikan bilangan negatif menghasilkan bilangan positif. Untuk itu, kita perlu mengingat beberapa hal, antara lain :
1. Bilangan apapun dan berapapun, jika dikalikan dengan 0, hasilnya adalah 0
contoh: a x 0 = 0
2. Bilangan apapun dan berapapun, jika dijumlahkan dengan lawannya, hasilnya adalah 0
contoh: 5 + (-5) = 0, -5 adalah lawan dari 5 dan sebaliknya
3. Berlaku sifat distribusi pada perkalian terhadap penjumlahan, termasuk di dalamnya perkalian bilangan negatif.

ambil sebarang bilangan a dan b,
a memiliki lawan -a dan b memiliki lawan -b,
-a x 0 = 0
-a x (b +(-b)) = 0, ( b dijumlahkan dengan -b menghasilkan 0)
(-axb) + (-a x -b) = 0 (sifat distributif pada perkalian)
Karena pada saat -a xb dijumlahkan dengan -a x -b menghasilkan 0, berarti -a x -b adalah lawan dari -a x b.
Padahal -a x b (perkalian bilangan negatif dengan positif) menghasilkan bilangan negatif,
berarti -a x -b (adalah lawan dari -a x b)akan menghasilkan bilangan positif.

Terbuktilah bahwa bilangan negatif dikalikan bilangan negatif menghasilkan bilangan positif.

Contoh :
-3 x 0 = 0
-3 x (5+(-5)) = 0
(-3 x 5) + (-3 x -5) = 0

-3 x -5 adalah lawan dari -3 x 5, padahal -3 x 5 menghasilkan bilangan -15 (negatif), berarti dapat dipastikan -3 x -5 = 15 (positif/ kebalikan dari lawannya)

Bagaimana para siswa?? apakah membingungkan tulisan saya?? Mari kita berdiskusi...^_^